Исследование зависимости вязкости растворов от концентрации с помощью вискозиметра. измерение вязкости крови: учебно-методическая разработка лабораторной работы по курсу «медицинская и биологическая ф

Типы вискозиметров

В зависимости от способа измерения вискозиметры подразделяются на капиллярные (вискозиметры истечения), шариковые, ротационные, вибрационные и ультразвуковые.

При пользовании капиллярными вискозиметрами измеряется время истечения известного количества (объема) жидкости сквозь капиллярные трубки определенного диаметра. Стеклянные капиллярные вискозиметры чаще других используются в практике химических лабораторий.

При пользовании шариковыми вискозиметрами измеряется скорость падения шарика в исследуемой жидкости — она тем меньше, чем больше вязкость жидкости.

В ротационных вискозиметрах измеряется крутящий момент или угловая скорость вращения одного из двух соосных тел, в зазоре между которыми находится испытуемая жидкость. Область измерения вязкости 0,5-1000000 Па*с. Они широко используются для определения вязкости высокомолекулярных жидкостей и растворов полимерных соединений.

Измерение вязкости вибрационными вискозиметрами основано на зависимости амплитуды колебаний тела в исследуемой жидкости от ее вязкости.

Ультразвуковыми вискозиметрами измеряют скорость затухания колебаний магнитострикционного материала, помещенного в исследуемую жидкость.

Независимо от конструкции вискозиметра, определение вязкости следует проводить в условиях строгого термостатирования.

Вязкость. Пояснения. Абсолютная и кинематическая вязкость. Таблицы значений вязкости — мало, школьный вариант. Вариант для печати.

• Кинематическая вязкость — мера потока имеющей сопротивление жидкости под влиянием силы тяжести. Когда две жидкости равного объема помещены в идентичные капиллярные вискозиметры и двигаются самотеком, вязкой жидкости требуется больше времени для протекания через капилляр. Если одной жидкости требуется для вытекания 200 секунд,а другой — 400 секунд, вторая жидкость в два раза более вязкая, чем первая по шкале кинематической вязкости.
  • Размерность кинематической вязкости — L2/T, где L — длина, и T — время. Обычно используется сантистокс (cSt). ЕДИНИЦА СИ кинематической вязкости — mm2/s, = 1 cSt =1 сантиСтокс = 10-6м2/с = мм2/с
  • Перевод единиц кинематической вязкости

• Абсолютная (динамическая) вязкость, иногда называемая динамической или простой вязкостью, является произведением кинематической вязкости и плотности жидкости:
  • Абсолютная вязкость = Кинематическая вязкость * Плотность
  • Абсолютная вязкость выражается в сантипуазах (сПуаз). ЕДИНИЦА СИ абсолютной вязкости — Паскаль-секунда (Pa-s), запомним, что 1 сПуаз = 1 mPa-s.
  • Перевод единиц динамической = абсолютной вязкости

Вязкость газов при атмосферном давлении: η, 10 -6 Па· с 150 К 200 К 250 К 300 К 400 К Азот 10.0 12.9 15.5 17.9 22.1 Аммиак — 6.89 8.53 10.3 13.9 Аргон 12.3 16.0 19.5 22.7 28.5 Ацетилен — — — 10.3 13.5 Бромметан — — 13.2 15.8 20.2 Водород 5.57 6.78 7.90 8.94 10.9 Водяной пар — — — 9.13 13.2 Воздух 10.3 13.2 16.0 18.5 23.0 Гелий 12.3 15.0 17.5 19.9 24.3 Кислород 11.3 14.6 17.8 20.7 25.9 Метан — 7.76 9.53 11.2 14.2 Неон 19.4 23.9 28.0 31.7 38.4 Оксид азота (II) 10.5 13.6 16.6 19.3 24.1 Оксид углерода (II) 9.84 12.7 15.4 17.8 22.1 Оксид углерода (IV) — 10.2 12.6 15.0 19.5 Пропан — — 7.1 8.3 9.5 Этан — 6.43 7.96 9.45 12.2 Этилен — 7.1 8.8 10.4 13.5	Вязкость жидкостей при атмосферном давлении: η, 10 -3 Па· с 0°C 20°C 50°C 70°C 100°C Ацетон = 0.32 0.25 = = Бензин 0.73 0.52 0.37 0.26 0.22 Бензол = 0.65 0.44 0.35 = Вода 1.80 1.01 0.55 0.41 0.28 Глицерин 12100 1480 180 59 13 Керосин 2.2 1.5 0.95 0.75 0.54 Кислота уксусная = 1.2 0.62 0.50 0.38 Масло касторовое = 987 129 49 = Пентан 0.28 0.24 = = = Ртуть = 1.54 1.40 = 1.24 Спирт метиловый 0.82 0.58 0.4 0.3 0.2 Спирт этиловый (96%) 1.8 1.2 0.7 0.5 0.3 Толуол = 0.61 0.45 0.37 0.29	Вязкость расплавов: t°, °C η, 10 -3 Па· с Алюминий 700 2.90 Висмут 305 1.65 Калий 100 0.46 Натрий 105 0.69 Олово 240 1.91 Свинец 440 2.11 Цинк 430 3.3 Бромид ртути 250 3.0 Бромид свинца 380 10.2 Бромид серебра 610 1.86 Гидроксид калия 400 2.3 Гидроксид натрия 350 4.0 Хлорид калия 790 1.4 Хлорид натрия 320 2.83 Хлорид серебра 600 1.61
Вязкость воды: t°, °C η, 10 -6 Па· с 1797 10 1307 20 1004 30 803 40 655 50 551 60 470 70 407 80 357 90 317 100 284 110 256 120 232 130 212 140 196 150 184	Динамическая вязкость воздуха: η, 10 -6 Па· с температура воздуха давление 0°C 25°C 100°C 1 атм 17.20 18.37 21.80 20 атм 17.53 18.65 22.02 50 атм 18.15 19.22 22.40 100 атм 19.70 20.60 23.35 200 атм 23.70 23.95 25.30

Вязкость сахарного сиропа

Сахаром в быту называется сахароза. Свекловичный и тростниковый сахар (в виде песка и рафинада) — очень важный продукт питания. Сахароза относится к углеводам, питательным веществам, заряжающим организм энергией.

Сахарный сироп (основа многих мучных и кондитерских изделий) обладает определенной вязкостью. Она есть уже у самой воды, в составе данной среды. С повышением концентрации растворов вязкость сиропов увеличивается. При концентрации сахара свыше 80 % начинается процесс кристаллизации сахара.

Выделяют следующие разновидности сиропов.

1. Сахарно-паточный. Помимо растворенного в воде сахара содержит патоку. Имеет более высокую вязкость.

2. Инвертный. Обладает более низкой вязкостью, но повышенной гигроскопичностью.

3. Молочный. Растворителем здесь служит молоко (цельное, сухое, сгущенное, сливки), возможно добавление патоки. Данный сироп выступает основным полуфабрикатом при изготовлении молочных конфет, помадных масс.

Для перекачивания сиропов лучше всего подходят центробежные и кулачковые насосы.

Физические свойства воды при температуре от 0 до 100°С

В таблице представлены следующие физические свойства воды: плотность воды ρ, удельная энтальпия h, удельная теплоемкость C_p, теплопроводность воды λ, температуропроводность воды а, вязкость динамическая μ, вязкость кинематическая ν, коэффициент объемного теплового расширения β, коэффициент поверхностного натяжения σ, число Прандтля Pr. Физические свойства воды приведены в таблице при нормальном атмосферном давлении в интервале от 0 до 100°С.

Физические свойства воды существенно зависят от ее температуры. Наиболее сильно эта зависимость выражена у таких свойств, как удельная энтальпия и динамическая вязкость. При нагревании значение энтальпии воды значительно увеличивается, а вязкость существенно снижается. Другие физические свойства воды, например, коэффициент поверхностного натяжения, число Прандтля и плотность уменьшаются при росте ее температуры. К примеру, плотность воды при нормальных условиях (20°С) имеет значение 998,2 кг/м3, а при температуре кипения снижается до 958,4 кг/м3.

Такое свойство воды, как теплопроводность (или правильнее — коэффициент теплопроводности) при нагревании имеет тенденцию к увеличению. Теплопроводность воды при температуре кипения 100°С достигает значения 0,683 Вт/(м·град). Температуропроводность H₂O также увеличивается при росте ее температуры.

Следует отметить нелинейное поведение кривой зависимости удельной теплоемкости этой жидкости от температуры. Ее значение снижается в интервале от 0 до 40°С, затем происходит постепенный рост теплоемкости до величины 4220 Дж/(кг·град) при 100°С.

Физические свойства воды при атмосферном давлении — таблица

t, °С →	10	20	30	40	50	60	70	80	90	100
ρ, кг/м3	999,8	999,7	998,2	995,7	992,2	988	983,2	977,8	971,8	965,3	958,4
h, кДж/кг	42,04	83,91	125,7	167,5	209,3	251,1	293	335	377	419,1
Cp, Дж/(кг·град)	4217	4191	4183	4174	4174	4181	4182	4187	4195	4208	4220
λ, Вт/(м·град)	0,569	0,574	0,599	0,618	0,635	0,648	0,659	0,668	0,674	0,68	0,683
a·108, м2/с	13,2	13,7	14,3	14,9	15,3	15,7	16	16,3	16,6	16,8	16,9
μ·106, Па·с	1788	1306	1004	801,5	653,3	549,4	469,9	406,1	355,1	314,9	282,5
ν·106, м2/с	1,789	1,306	1,006	0,805	0,659	0,556	0,478	0,415	0,365	0,326	0,295
β·104, град-1	-0,63	0,7	1,82	3,21	3,87	4,49	5,11	5,7	6,32	6,95	7,52
σ·104, Н/м	756,4	741,6	726,9	712,2	696,5	676,9	662,2	643,5	625,9	607,2	588,6
Pr	13,5	9,52	7,02	5,42	4,31	3,54	2,93	2,55	2,21	1,95	1,75

Примечание: Температуропроводность в таблице дана в степени 108 , вязкость в степени 106 и т. д. для других свойств. Размерность физических свойств воды выражена в единицах СИ.

Вязкость жидкостей

Динамическая вязкость

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Для так называемых ньютоновских жидкостей (которых вокруг нас большинство) справедлив общий закон внутреннего трения — закон Ньютона:

τ=−η∂v∂n.{\displaystyle \tau =-\eta {\frac {\partial v}{\partial n}}.}

Коэффициент вязкости η{\displaystyle \eta } (коэффициент динамической вязкости, динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что η{\displaystyle \eta } будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля — Андраде:

η=CewkT.{\displaystyle \eta =Ce^{w/kT}.}

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества VM{\displaystyle V_{M}}. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

η=cVM−VC,{\displaystyle \eta ={\frac {c}{V_{M}-V_{C}}},}

где:

c{\displaystyle c} — константа, характерная для определенной жидкости;

VC{\displaystyle V_{C}} — собственный объём, занимаемый частицами жидкости.

Динамическая вязкость жидкостей уменьшается с увеличением температуры и растёт с увеличением давления.

Кинематическая вязкость

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

ν=ηρ,{\displaystyle \nu ={\frac {\eta }{\rho }},}

и эта величина получила название кинематической вязкости.

Здесь ρ{\displaystyle \rho } — плотность жидкости; η{\displaystyle \eta } — коэффициент динамической вязкости.

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом: 1 сСт = 1 мм2/c = 10−6 м2/c.

Условная вязкость

Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 мл испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 мл дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле

ν=7,4⋅10−6Et,{\displaystyle \nu =7,4\cdot 10^{-6}E_{t},}

где ν{\displaystyle \nu } — кинематическая вязкость (в м2/с), а Et{\displaystyle E_{t}} — условная вязкость (в °ВУ) при температуре t.

Ньютоновские и неньютоновские жидкости

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса):

σij=η(∂vi∂xj+∂vj∂xi),{\displaystyle \sigma _{ij}=\eta \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}\right),}

где σi,j{\displaystyle \sigma _{i,j}} — тензор вязких напряжений.

Среди неньютоновских жидкостей по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.[источник не указан 407 дней]

Вязкость аморфных материалов

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс:

η ( T ) = A ⋅ exp ⁡ ( Q R T ) , {\displaystyle \eta (T)=A\cdot \exp \left({\frac {Q}{RT}}\right),}

где:

• Q {\displaystyle Q} — энергия активации вязкости (Дж/моль);
• T {\displaystyle T} — температура ();
• R {\displaystyle R} — универсальная газовая постоянная (8,31 Дж/моль·К);
• A {\displaystyle A} — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q {\displaystyle Q} изменяется от большой величины Q H {\displaystyle Q_{H}} при низких температурах (в стеклообразном состоянии) на малую величину Q L {\displaystyle Q_{L}} при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда ( Q H − Q L ) < Q L {\displaystyle \left(Q_{H}-Q_{L}\right) , или ломкие, когда ( Q H − Q L ) ≥ Q L {\displaystyle \left(Q_{H}-Q_{L}\right)\geq Q_{L}} . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса R D = Q H Q L {\displaystyle R_{D}={\frac {Q_{H}}{Q_{L}}}} : сильные материалы имеют R D < 2 {\displaystyle R_{D}<2} , в то время как ломкие материалы имеют R D ≥ 2 {\displaystyle R_{D}\geq 2} .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:

η ( T ) = A 1 ⋅ T ⋅ ⋅ {\displaystyle \eta (T)=A_{1}\cdot T\cdot \left\cdot \left}

с постоянными A 1 {\displaystyle A_{1}} , A 2 {\displaystyle A_{2}} , B {\displaystyle B} , C {\displaystyle C} и D {\displaystyle D} , связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования T g {\displaystyle T_{g}} это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Вязкость

Если температура существенно ниже температуры стеклования T < T g {\displaystyle T , двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

η ( T ) = A L T ⋅ exp ⁡ ( Q H R T ) , {\displaystyle \eta (T)=A_{L}T\cdot \exp \left({\frac {Q_{H}}{RT}}\right),}

с высокой энергией активации Q H = H d + H m {\displaystyle Q_{H}=H_{d}+H_{m}} , где H d {\displaystyle H_{d}} — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а H m {\displaystyle H_{m}} — энтальпия их движения. Это связано с тем, что при T < T g {\displaystyle T аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При T ≫ T g {\displaystyle T\gg T_{g}} двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

η ( T ) = A H T ⋅ exp ⁡ ( Q L R T ) , {\displaystyle \eta (T)=A_{H}T\cdot \exp \left({\frac {Q_{L}}{RT}}\right),}

но с низкой энергией активации Q L = H m {\displaystyle Q_{L}=H_{m}} . Это связано с тем, что при T ≫ T g {\displaystyle T\gg T_{g}} аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Вязкость грунта

Грунт — многокомпонентное геологическое образование, включающее в себя почвы, различные горные породы, являющееся объектом инженерно-строительной деятельности человека.

Вязкость грунтов определяет их сопротивление течению под воздействием внешних сил. Этот показатель зависит от их структуры, химико-минералогического состава. Коэффициент вязкости для грунтов разного типа колеблется в широких диапазонах: от 102–104 пз для илов до 1022 пз для известняка. С увеличением плотности грунта его вязкость, а кроме того, порог ползучести увеличиваются.

По величине вязкости данной среды выделяются:

• наименее вязкие горные породы (тощие глины, гипсы, соли, тонкослоистые алевролито-глинистые толщи);
• слабовязкие породы (песчано-глинистые, тонкослоистые известняково-мергелистые, флишевые толщи);
• сильно вязкие породы (слабослоистые песчаниковые, конгломератовые, карбонатные, вулканогенные);
• наиболее вязкие породы (кристаллические сланцы, граниты, гнейсы).

Вязкость газа

Вязкость чистых газов и смесей может быть рассчитана по методу Чепмена-Энскога с использованием потенциала взаимодействия молекула-молекула, такого как потенциал Леннарда-Джонса . Это свойство макроскопического транспортное (непрерывный домен) является образом передач импульса на молекулярном уровне , которые увеличивают с силой столкновений, следовательно , с температурой , и которые выступают против адвекции этого импульса. В середине.

Чистая субстанция

Динамическая вязкость чистого тела определяется следующим выражением (индексы относятся к столкновению вида i с самим собой)

ηязнак равноα(MяТ)12σяяΩяя*,αзнак равно516(kBπНЕТВ)12знак равно8.4419 …×10-25J12⋅K-12⋅мол12{\ displaystyle \ eta _ {i} = \ alpha {\ frac {(M_ {i} T) ^ {\ frac {1} {2}}} {\ sigma _ {ii} \ Omega _ {ii} ^ { *}}} \ ,, \ quad \ alpha = {\ frac {5} {16}} \ left ({\ frac {k_ {B}} {\ pi N_ {A}}} \ right) ^ {\ frac {1} {2}} = 8,4419 … \ times 10 ^ {- 25} \, J ^ {\ frac {1} {2}} \ cdot K ^ {- {\ frac {1} {2}} } \ cdot mol ^ {\ frac {1} {2}}}

где это температура, молекулярная масса , число Авогадро , постоянная Больцмана , сечение и интеграл столкновений уменьшается на его стоимости с использованием потенциальных твердых сфер . Этот член слабо зависит от температуры, поэтому он близок к единице. Если мы возьмем, то найдем приближение среды, состоящей из идеально упругих твердых сфер . Термин представляет количество столкновений в единицу времени.
Т{\ displaystyle T}Mя{\ displaystyle M_ {i}}НЕТВ{\ displaystyle N_ {A}}kB{\ displaystyle k_ {B}}σяя{\ displaystyle \ sigma _ {ii}}Ωяя*{\ displaystyle \ Omega _ {ii} ^ {*}}Ωяя*знак равно1{\ displaystyle \ Omega _ {ii} ^ {*} = 1}Т12{\ displaystyle T ^ {\ frac {1} {2}}}

Количество часто доступно в базах данных в виде таблицы или полиномиальной формы.
σΩ*{\ Displaystyle \ sigma \ Omega ^ {*}}

узнак равно∑язнак равноя1я2вяТя{\ displaystyle y = \ sum _ {i = i_ {1}} ^ {i_ {2}} a_ {i} T ^ {i}}

где может быть отрицательным.
я1{\ displaystyle i_ {1}}

Этот тип приближения также используется для получения числового выражения .
ηзнак равнож(Т){\ displaystyle \ eta = f (T)}

Газовые смеси

Различное приближение вязкости воздуха до 10000К.

Динамическая вязкость газовой смеси тел является решением линейной алгебраической системы порядка и ранга . Поэтому он выражается в виде где — массовая доля вещества в смеси. Существует ряд точных приближений в более или менее широкой области (см. Рисунок напротив):
НЕТ{\ displaystyle N}НЕТ{\ displaystyle N} НЕТ-1{\ displaystyle N-1}ηзнак равнож(Т,противя(Т)){\ displaystyle \ eta = f \ left (T, c_ {i} (T) \ right)}противя{\ displaystyle c_ {i}}я{\ displaystyle i}

• некоторые, немного сложные, но теоретически обоснованные, например, у Будденберга и Вильке, дают отличные результаты;
• простой закон смешивания дает приемлемые результаты в ограниченном диапазоне температур. Написан такой эмпирический закон:

η-1знак равно∑противяηя-1{\ displaystyle \ eta ^ {- 1} = \ sum c_ {i} \ eta _ {i} ^ {- 1}}

Обычно используется закон Сазерленда , который представляет собой численную адаптацию теоретической модели с использованием определенного потенциала взаимодействия.

Цифровые данные

Многочисленные и достоверные данные содержатся в сборнике Ерама Саркиса Тулукяна . Некоторые значения этой базы данных приведены в таблице ниже.

Тело	Вязкость ( Па с )
водород
8,79 × 10 −6
диазот	1,754 × 10 −5
водяной пар
8,85 × 10 −6

Вязкость муки

Мука — продукт, который получают посредством измельчения зерен с/х культур (в основном злаковых) до порошкообразной консистенции. На муку размалывают преимущественно пшеницу, рожь, в меньших объемах кукурузу, ячмень и прочие зерновые культуры.

Сила муки — показатель, определяющий ее хлебопекарные качества. Он обозначает, как поведет себя тесто при замесе, каким будет его вязкость, эластичность, упругость, водопоглотительная способность. В зависимости от реологических свойств теста классифицируют муку сильную, среднюю, слабую по силе.

Вязкость водно-мучной смеси обусловлена содержанием в муке клейковины, которая разбухает в растворенном виде.

Типы и характеристики моторных масел

В Европе, США, Японии и других странах действует маркировка моторных масел по  SAE  (Общество Автомобильных  Инженеров)по вязкости, похожая на классификацию, применяемую в России. Согласно классификации SAE масла делят на:

• Зимние масла при небольшой вязкости обеспе­чивают холодный пуск при низких температурах; но при высоких температурах не обеспечивают надеж­ного смазывания двигателя);
• Летние масла надежно смазывают двигатель при высоких температурах, но не обеспечивают холодный пуск при температуре воздуха ниже 0°С);
• Всесезонные масла при низких температурах обладают вязкостью зимних масел, а при высоких – летних.

Зимние масла обозначают буквой W (от слова winter -зима). SAE разделяет моторные масла на 10 клас­сов, отличающихся по вязкостно-температур­ным характеристикам. Типичные обозначения зимних масел – OW, 5W, 10W, 15W, 20W и 25W, летних – 20, 30, 40 и 50. Чем ниже число, указы­вающее класс зимнего масла, тем ниже темпе­ратура, при которой масло сохраняет работоспо­собность, т.е. смазывает трущиеся поверхности, свободно поступая к ним. Чем больше число в классе летнего масла, тем при более высоких температурах масло остается вязким, сохраняя устойчивую масляную пленку между трущимися деталями.

Функции моторного масла инфографика

Также  существует  принятая  во  многих  странах классификация API  (Американского  Нефтяного  Института), которая связывает эксплуатационные свойства масел с условиями работы двигателя. Условия применения масел обозначаются двумя буквами:

• первая определяет тип двигателя (S – бензиновый, С – дизель),
• вторая (А, В, С, D, E, F, G, Н) – уровень эксплуатационных свойств моторного масла.

Причем условия применения масла ужесточаются соответственно возрастанию порядкового номера буквы в алфавите. Масла классов SA и СА пред­назначены для нефорсированных двигателей, сконст­руированных до 70-х годов, работающих с легкими нагрузками. А масла классов SH и CD – для высоко-форсированных многоклапанных двигателей и двига­телей с наддувом, работающих в тяжелых условиях эксплуатации при высоких нагрузках (модели вы­пуска с 1989 года).

Инфографика Топ 10 покупаемых моторных масел в России

На упаковках обычно ставят обозначение маркировки моторного масла по обеим системам.

Тенденция такова, что масла в большинстве своем обычно изготавливают всесезонные. При этом мно­гие масла можно использовать как в бензиновых, так и в дизельных двигателях, однако последнее харак­терно только для моторных масел для легковых авто­мобилей.

Для упрощенной классификации моторные масла можно разделить на три большие группы, характе­ризующие состав масла. Масла бывают

• минеральные (полученные из нефтепродуктов),
• синтетические,
• полусинтетические (представляющие собой смесь двух первых).

Такое деление вполне оправдано, поскольку мине­ральные и синтетические масла отличаются по вяз­костно-температурным характеристикам, а значит – и по области применения и, что также немаловажно, по стоимости. Следует заметить, что большую роль играют всевозможные присадки, влияющие в первую очередь на свойства масла, а также и на его цену

Задачи на тему: Свойства газов

Задача №5.1.

Определить плотность воздуха при нормальных физических и стандартных условиях. Универсальная газовая постоянная для воздуха

Решение:

Нормальным физическим условиям соответствуют

Па, а стандартным

Из уравнения состояния идеального газа найдем плотности воздуха: при нормальных физических условиях

при стандартных условиях

Задача №5.2.

Два кислородных баллона одинакового объема соединены трубопроводом. Определить давление, которое установится в баллонах при температуре

если до соединения параметры газа в первом баллоне были:

а во втором

Решение:

Массу кислорода в каждом из баллонов до соединения определим, используя уравнение состояния идеального газа:

Общая масса кислорода в двух баллонах:

Тогда, давление в баллонах после их соединения

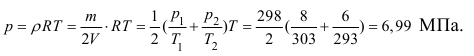
Задача №5.3.

Определить расход метана в газопроводе диаметром если скорость газа , абсолютное давление а температура 20 °С. Универсальная газовая постоянная метана

Решение:

Определим плотность газа:

Учитывая, что площадь сечения газопровода равна

найдем массовый расход газа:

Задача №5.4.

Какую мощность должен иметь электрический калорифер, чтобы нагревать при атмосферном давлении поток воздуха от до если производительность вентилятора по холодному воздуху Теплоемкость для воздуха принять равной 1,012 кДж/(кг-К).

Решение:

Определим массовый расход вентилятора

Тогда мощность калорифера

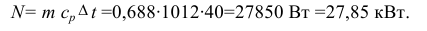
Задача №5.5.

Какое количество теплоты необходимо подвести к 1 кг воздуха с температурой 20 °С, чтобы его объем при постоянном давлении увеличился в 2 раза? Определить температуру воздуха в конце процесса. Теплоемкость воздуха = 1012 Дж/(кг-К).

Решение:

Для изобарического процесса

Поэтому конечная температура воздуха

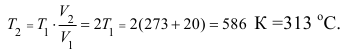
Изменение температуры при подводе тепла

Необходимое количество теплоты

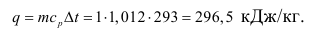
Задача №5.6.

Газ сжимается изотермически до десятикратного уменьшения объема. Определить конечное давление, если начальное равно 0,1 МПа.

Решение:

Для изотермического процесса

откуда

Задача №5.7.

В цилиндре под поршнем находится воздух при манометрическом давлении 0,02 МПа. Определить перемещение поршня и давление в конце процесса изотермического сжатия, если на поршень дополнительно действует груз массой 5 кг. Диаметр поршня . Высота начального положения поршня .

Решение:

Дополнительная сила, создаваемая грузом,

Дополнительное давление от груза:

Определим конечное давление

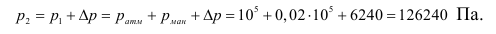
Объем воздуха в цилиндре до начала действия груза:

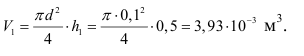
Объем воздуха после изотермического сжатия:

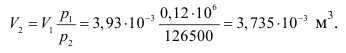
Тогда, высота положения поршня после сжатия

Ход поршня в цилиндре в результате сжатия

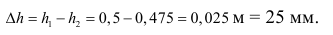
Задача №5.8.

При адиабатическом расширении 1 кг воздуха при температуре

давление понижается с

Определить параметры состояния газа в конце процесса расширения.

Решение:

Соотношение между параметрами состояния для адиабатического процесса

Подставив в это соотношение значения плотностей и для начального и конечного состояний

получим

Из полученного уравнения определим температуру в конце процесса адиабатического расширения:

а плотность воздуха в конце процесса расширения

Задача №5.9.

В баллоне находится углекислота, манометрическое давление которой а температура Определить изменение давления и температуры в баллоне, если из него выпустить половину (по массе) углекислоты. Процесс расширения газа в баллоне считать адиабатическим с показателем адиабаты Кстати готовые на продажу задачи тут, и там же теория из учебников возможно она вам поможет.

Решение:

Для адиабатического процесса справедливо соотношение:

Подставим в это соотношение значения давлений и из уравнения Клапейрона:

Тогда температура в конце адиабатического расширения

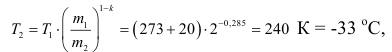
а абсолютное давление в баллоне

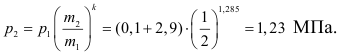
Избыточное давление в конце процесса расширения

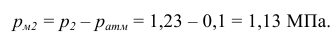
Задача №5.10.

При политропном сжатии 0,5 кг воздуха давление повышается от атмосферного до 1 МПа. Температура при этом увеличивается от 18 до 180 °С. Определить показатель политропы, а также объем воздуха в начале и конце процесса.

Решение:

Показатель политропы определяем по уравнению:

После логарифмирования этого уравнения получим:

Объем воздуха в начале процесса сжатия

а в конце

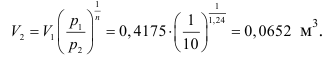
Эти страницы вам могут пригодиться:

1. Курсовая работа по гидравлике
2. Учебник по гидравлике
3. Формулы по гидравлике
4. Сборник задач по гидравлике

Теплопроводность воды в зависимости от температуры и давления

В таблице приведены значения теплопроводности воды и водяного пара при температурах от 0 до 700°С и давлении от 1 до 500 атм.

Как известно, вода при атмосферном давлении закипает и переходит в пар при температуре 100°С. Коэффициент теплопроводности воды в этих условиях равен 0,683 Вт/(м·град). При увеличении давления растет и температура кипения воды (закон Клапейрона — Клаузиуса). По данным таблицы видно, при давлении в 100 раз выше атмосферного (100 бар) вода находится в виде пара при температуре от 310°С и имеет теплопроводность 0,523 Вт/(м·град).

Таким образом, следует отметить, что изменение давления влияет как на температуру кипения воды, так и на величину ее теплопроводности. Высокая теплопроводность воды достигается за счет роста давления — при повышении давления коэффициент теплопроводности воды увеличивается. Например, при давлении 1 бар и температуре 20°С вода имеет теплопроводность, равную 0,603 Вт/(м·град). При росте давления до 500 бар теплопроводность воды становится равной 0,64 Вт/(м·град) при этой же температуре.

Примечание: Черта под значениями в таблице означает фазовый переход воды в пар, то есть цифры под чертой относятся к пару, а выше ее — к воде. Теплопроводность в таблице указана в степени 103. Не забудьте разделить на 1000! Размерность теплопроводности воды в таблице Вт/(м·град).

1. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей.
2. Михеев М.А., Михеева И.М. Основы теплопередачи.
3. Чубик И.А., Маслов А.М. Справочник по теплофизическим характеристикам пищевых продуктов и полуфабрикатов. М.: «Пищевая промышленность», 1970 — 184 с.
4. ГСССД 2-77 Вода. Плотность при атмосферном давлении и температурах от 0 до 100°С. М.: Издательство стандартов, 1978 — 6 с.

Плотность воды в зависимости от температуры

Принято считать, что плотность воды равна 1000 кг/м3, 1000 г/л или 1 г/мл, но часто ли мы задумываемся при какой температуре получены эти данные?

Максимальная плотность воды достигается при температуре 3,8…4,2°С. В этих условиях точное значение плотности воды составляет 999,972 кг/м3. Такая температурная зависимость плотности характерна только для воды. Другие распространенные жидкости не имеют максимума плотности на этой кривой — их плотность равномерно снижается по мере роста температуры.

Вода существует как отдельная жидкость в диапазоне температуры от 0 до максимальной 374,12°С — это ее критическая температура, при которой исчезает граница раздела между жидкостью и водяным паром. Значения плотность воды при этих температурах можно узнать в таблице ниже. Данные о плотности воды представлены в размерности кг/м3 и г/мл.

В таблице приведены значения плотности воды в кг/м3 и в г/мл (г/см3), допускается интерполяция данных. Например, плотность воды при температуре 25°С можно определить, как среднее значение от величин ее плотности при 24 и 26°С. Таким образом, при температуре 25°С вода имеет плотность 997,1 кг/м3 или 0,9971 г/мл.

Значения в таблице относятся к пресной или дистиллированной воде. Если рассматривать, например, морскую или соленую воду, то ее плотность будет выше — плотность морской воды равна 1030 кг/м3. Плотность соленой воды и водных растворов солей можно узнать в этой таблице. Плотность воды при различных температурах — таблица

t, °С	ρ, кг/м3	ρ, г/мл	t, °С	ρ, кг/м3	ρ, г/мл	t, °С	ρ, кг/м3	ρ, г/мл
999,8	0,9998	62	982,1	0,9821	200	864,7	0,8647
0,1	999,8	0,9998	64	981,1	0,9811	210	852,8	0,8528
2	999,9	0,9999	66	980	0,98	220	840,3	0,8403
4	1000	1	68	978,9	0,9789	230	827,3	0,8273
6	999,9	0,9999	70	977,8	0,9778	240	813,6	0,8136
8	999,9	0,9999	72	976,6	0,9766	250	799,2	0,7992
10	999,7	0,9997	74	975,4	0,9754	260	783,9	0,7839
12	999,5	0,9995	76	974,2	0,9742	270	767,8	0,7678
14	999,2	0,9992	78	973	0,973	280	750,5	0,7505
16	999	0,999	80	971,8	0,9718	290	732,1	0,7321
18	998,6	0,9986	82	970,5	0,9705	300	712,2	0,7122
20	998,2	0,9982	84	969,3	0,9693	305	701,7	0,7017
22	997,8	0,9978	86	967,8	0,9678	310	690,6	0,6906
24	997,3	0,9973	88	966,6	0,9666	315	679,1	0,6791
26	996,8	0,9968	90	965,3	0,9653	320	666,9	0,6669
28	996,2	0,9962	92	963,9	0,9639	325	654,1	0,6541
30	995,7	0,9957	94	962,6	0,9626	330	640,5	0,6405
32	995	0,995	96	961,2	0,9612	335	625,9	0,6259
34	994,4	0,9944	98	959,8	0,9598	340	610,1	0,6101
36	993,7	0,9937	100	958,4	0,9584	345	593,2	0,5932
38	993	0,993	105	954,5	0,9545	350	574,5	0,5745
40	992,2	0,9922	110	950,7	0,9507	355	553,3	0,5533
42	991,4	0,9914	115	946,8	0,9468	360	528,3	0,5283
44	990,6	0,9906	120	942,9	0,9429	362	516,6	0,5166
46	989,8	0,9898	125	938,8	0,9388	364	503,5	0,5035
48	988,9	0,9889	130	934,6	0,9346	366	488,5	0,4885
50	988	0,988	140	925,8	0,9258	368	470,6	0,4706
52	987,1	0,9871	150	916,8	0,9168	370	448,4	0,4484
54	986,2	0,9862	160	907,3	0,9073	371	435,2	0,4352
56	985,2	0,9852	170	897,3	0,8973	372	418,1	0,4181
58	984,2	0,9842	180	886,9	0,8869	373	396,2	0,3962
60	983,2	0,9832	190	876	0,876	374,12	317,8	0,3178

Следует отметить, что при увеличении температуры воды (выше 4°С) ее плотность уменьшается. Например, по данным таблицы, плотность воды при температуре 20°С равна 998,2 кг/м3, а при ее нагревании до 90°С, величина плотности снижается до значения 965,3 кг/м3. Удельная масса воды при нормальных условиях значительно отличается от ее плотности при высоких температурах. Средняя плотность воды, находящейся при температуре 200…370°С намного меньше ее плотности в обычном температурном диапазоне от 0 до 100°С.

Смена агрегатного состояния воды приводит к существенному изменению ее плотности. Так, величина плотности льда при 0°С имеет значение 916…920 кг/м3, а плотность водяного пара составляет величину в сотые доли килограмма на кубический метр. Следует отметить, что значение плотности воды почти в 1000 раз больше плотности воздуха при нормальных условиях.

Кроме того, вы также можете ознакомиться с таблицей плотности веществ и материалов.

Вязкость воска

Воск как продукт восковых желез пчел представляет собой смесь сложных эфиров жирных кислот и высших спиртов. По своим физическим свойствам это твердая, мелкозернистая в изломе субстанция (при комнатной температуре) с окраской, которая варьируется от коричневой до практически бесцветной. Воск нерастворим в воде, плохо растворяется в спиртах, но при нагревании полностью растворяется в некоторых жидкостях (бензине, скипидаре, эфире, ацетоне, животных жирах, жирных маслах).

Кроме животного воска, существуют природные растительные и минеральные воски, по своим свойствам близкие к пчелиному. Пример первых — воск пальмовых листьев (карнаубский воск), пример вторых — парафин, нефтяные отложения. Также данный продукт синтезируют искусственным путем.

Наибольшей вязкостью воск обладает при температуре, близкой к температуре его застывания. Причем при 100 °С вязкость воска снижается вдвое, но все равно она значительно больше, чем у воды.